sú funkcie
Funkcie sínus a kosínus majú definičný obor  a
sú periodické s periódou
a
sú periodické s periódou  . Funkcia sínus je nepárna, funkcia
kosínus je párna.
. Funkcia sínus je nepárna, funkcia
kosínus je párna.
Obrázok:
Graf funkcie 
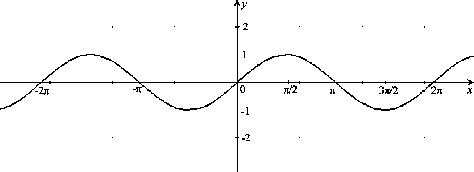 |
Obrázok:
Graf funkcie 
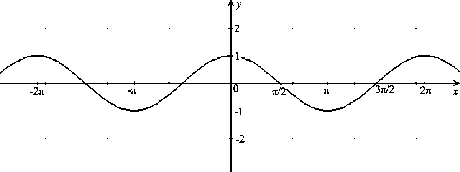 |
Funkcie tangens a kotangens sú nepárne, periodické
funkcie s periódou  .
Pre ich definičné obory platí
.
Pre ich definičné obory platí
 ,
,  a
a
 ,
,  .
.
Obrázok:
Graf funkcie

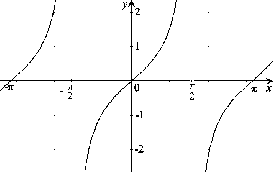 |
Obrázok:
Graf funkcie

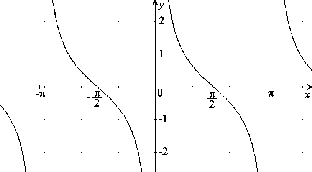 |
Funkcie sekans a kosekans sú definované pomocou funkcií sínus a
kosínus vz»ahmi
Obrázok:
Graf funkcie 
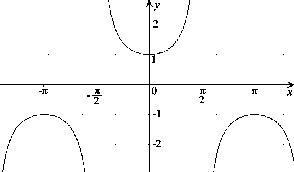 |
Obrázok:
Graf funkcie

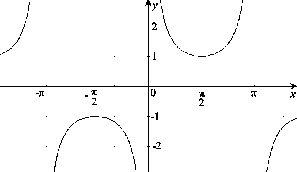 |
![]() .
Pre ich definičné obory platí
.
Pre ich definičné obory platí
![]() ,
, ![]() a
a
![]() ,
, ![]() .
.